Qndev’s blog
About me
The Geometry of Linear Equations [1]
by NGUYEN DINH QUANG
The geometry of linear equations - Ý nghĩa hình học của phương trình tuyến tính
Vấn đề cơ bản của đại số tuyến tính là giải hệ phương trình tuyến tính với \(n\) ẩn số; ví dụ:
\[
\left\{\begin{matrix}
2x - y = 0\
-x + 2y = 3
\end{matrix}\right.
\]
Chúng ta sẽ tìm hiểu vấn đề này theo 3 cách. Hệ bên trên là hệ phương trình tuyến tính tring không gian vector hai chiều \((n=2)\).
Row Picture
Nghiệm của hệ phương trình tuyến tính trên chính là giao điểm của hai đường thẳng đại diện cho hai phương trình trong hệ đó. Nhìn vào bức ảnh dưới đay ta có thể thấy \(x=1\), \(y=2\) là nghiệm của hệ phương trình.
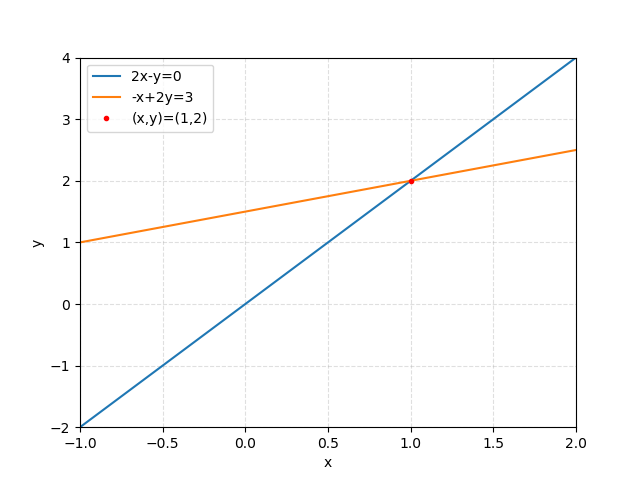
Để kiểm chứng lại nghiệm đó ta thây \((x,y)=(1,2)\) vào hệ:
\[
\left\{\begin{matrix}
2.1 - 2 = 0\
-1 + 2.2 = 3
\end{matrix}\right.
\]
Nghiệm của hệ phương trình tuyến tính trong không gian ba chiều là giao điểm của ba mặt phẳng(nếu hệ có nghiệm).
Column Picture
Chúng ta sẽ xem hệ phương trình tuyến tính giống như một phương trình bằng cách biến các hệ số thành các vector:
\[
x\begin{bmatrix}
2 \
-1
\end{bmatrix}+y\begin{bmatrix}
-1 \
2
\end{bmatrix}=\begin{bmatrix}
0 \
3
\end{bmatrix}
\]
Cho hai vectors \(c\) và \(d\) và các số vô hướng \(x\) và \(y\), tổng \(xc+yd\) được gọi là tổ hợp tuyến tính của \(c\) và \(d\).
Với \(x=1\) và \(y=2\) thì tổ hợp tuyến tính của hai vector \(\begin{bmatrix}2 \\ -1\end{bmatrix}\) và \(\begin{bmatrix}1 \\ -2\end{bmatrix}\) sẽ bằng vector \(\\(\begin{bmatrix}0 \\ 3\end{bmatrix}\)) được biểu diễn bằng hình ảnh dưới đây:
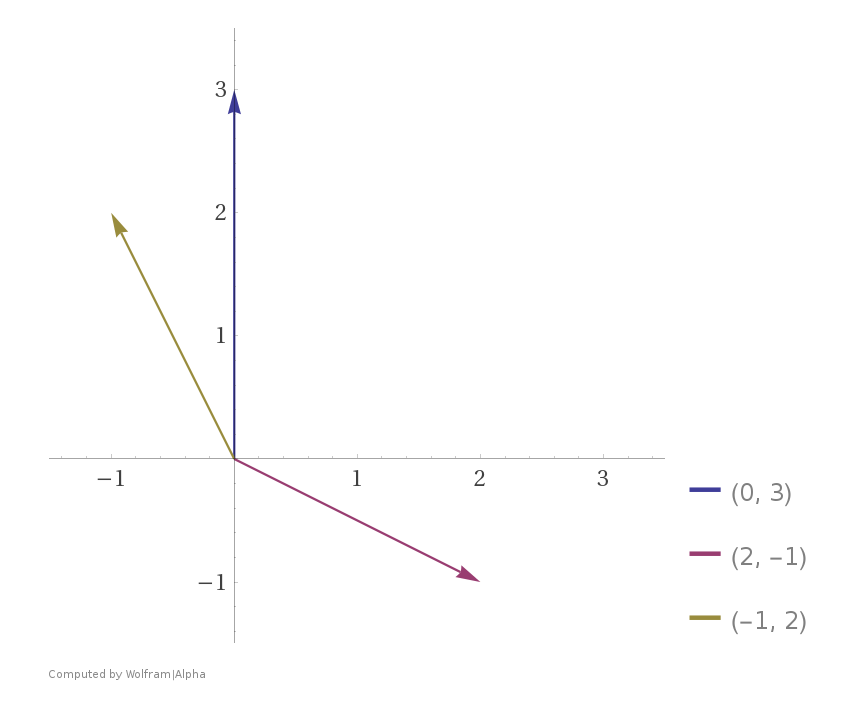
Trong không gian vector ba chiều column picture yêu cầu chúng ta phải tìm kiếm một tổ hợp tuyến tính của các vector 3 chiều sao cho chúng bằng vector \(b\).
Matrix Picture
Chúng ta sẽ viết hệ phương trình tuyến tính \(\left\{\begin{matrix}2x - y = 0 \\ -x + 2y = 3\end{matrix}\right.\) thành một phương trình bằng cách sử dụng ma trận và vector:
\[ \begin{bmatrix}2 & -1\\ -1 & 2\end{bmatrix}\begin{bmatrix}x \\ y\end{bmatrix}=\begin{bmatrix}0 \\ 3\end{bmatrix} \]
Ma trận \(A=\begin{bmatrix}2 & -1\\ -1 & 2\end{bmatrix}\) được gọi là ma trận hệ số. Vector \(x=\begin{bmatrix}x \\ y\end{bmatrix}\) là vector của ẩn số. Các giá trị phía bên tay phải của phương trình là vector \(b\) \[Ax=b.\]
Không gian ba chiều của matrix picture cũng giống như hai chiều ngoại trừ việc kích cỡ của vector và matrix được tăng lên.
Matrix Multiplication
Làm sao chúng ta có thể nhân một ma trận \(A\) với một vector \(x\)?
\[ \begin{bmatrix}2 & 5\\ 1 & 3\end{bmatrix}\begin{bmatrix}1 \\ 2\end{bmatrix}=\;? \]
Một cách mà ta có thể nghĩ tới đó là phần tử của \(x\) giống như các hệ số của một tổ hợp tuyến tính của các vector cột của ma trận:
\[ \begin{bmatrix}2 & 5\\ 1 & 3\end{bmatrix}\begin{bmatrix}1 \\ 2\end{bmatrix}=1\begin{bmatrix}1 \\ 2\end{bmatrix}+2\begin{bmatrix}5 \\ 3\end{bmatrix}=\begin{bmatrix}12 \\ 7\end{bmatrix} \]
Kỹ thuật này sẽ biểu diễn \(Ax\) là một tổ hợp tuyến tính các cột của \(A\). Bạn cũng có thể thực hiện việc tính toán phép nhân \(Ax\) bằng cách nhân từng hàng của ma trận \(A\) với vector \(x\):
\[ \begin{bmatrix}2 & 5\\ 1 & 3\end{bmatrix}\begin{bmatrix}1 \\ 2\end{bmatrix}=\begin{bmatrix}2.1 + 5.2\\ 1.1 + 3.2\end{bmatrix}=\begin{bmatrix}12 \\ 7\end{bmatrix} \]
Linear Independence
Trong cột và bức tranh về ma trận, bên phải của phương trình là vector \(b\). Cho ma trận \(A\), chúng ta có thể giải được phương trình: \[Ax=b\] với mọi vector \(b\)? Hay nói cách khác là tổ hượp tuyến tính của các vector cột có thể bao phủ hết mặt phẳng tọa độ \(xy\) (hoặc không gian trong trường hợp không gian ba chiều)? Nếu câu trả lời là không, chúng ta gọi \(A\) là ma trận suy biến. Trong trường hợp này các vector cột của nó là phụ thuộc tuyến tính; tất cả các tổ hợp tuyến tính nằm trên một điểm, đường thẳng (trong không gian hai chiều) hoặc trên một điểm, đường thẳng, mặt phẳng (trong không gian ba chiều). Các tổ hợp không bao phủ, lấp đầy toàn bộ không gian.
18.06SC Linear Algebra / Fall 2011