Qndev’s blog
About me
Phương trình tuyến tính trong đại số tuyến tính - Notes
by NGUYEN DINH QUANG
Hệ phương trình tuyến tính
Một phương trình tuyến tính với các biến \(x_1,x_2,x_3,…,x_n\) trong phưowng trình có thể viết dưới dạng: \[a_1x_1 + a_2x_2 + … + a_nx_n = b \tag{1}\] trong đó \(b\) và các hệ số \(a_1,a_2,…,a_n\) là các số thực. Các chỉ số \(n\) là các số nguyên dương. Ví dụ: Các phương trình: \[-x_1 + 15x_1 + 4x_2 = 1996 \; và \; x_2 = 28x_1 +2x_3 + 15\] là các phương trình tuyến tính bởi khi ta rút gọn chúng lạ ta có \(14x_1 + 4x_2 = 1996 \; và \; 28x_1 - x_2 +2x_3 = -15 \)có dạng (1). Các phương trình: \(4x_1 - 5x_2 = x_1x_2 \; và \; x_2 = 2\sqrt{x_1} -6\) không phải là các phương trình tuyến tính.
Hệ phương trình tuyến tính hay hệ tuyến tính là tổ hợp của một hoặc nhiều phương trình tuyến tính có liên quan đến các biến giống nhau được gọi là \(x_1,x_2,…,x_n \). Ví dụ: Ta có hệ phương trình: \[\begin{cases} 2x_1 - x_2 + 1.5x_3 = 8 \\ x_1 + 0x_2 - 4x_3 = -7 \end{cases} \tag{2}\]
Lời giải của hệ là danh sách \((s_1,s_2,s_3,…,s_n)\) các số mà tại đó làm thoả mãn từng phương trình trong hệ (các giá trị \(s_1,s_2,s_3,…,s_n\)) thay thế tương ứng chó các biến (\(x_1,x_2,x_3,…,x_n\)). Ví dụ: \((5,6.5,3)\) là lời giải cho hệ phương trình (2) bởi vì khi thay thế các số thực trên tương ứng với \(x_1,x_2,x_3\) của hệ ta được các phương trình luôn đúng: \(8 = 8 \; và -7 = -7\).
Tất cả các lời giải có thể thoả mãn hệ được gọi là tập lời giải (tập nghiệm). Hai hệ phương trình tuyến tính được gọi là tương đương nhau nếu chúng có cùng tập nghiệm.
Chú ý: Một hệ phương trình tuyến tính có thể có: không có nghiệm hoặc có chính xác một nghiệm duy nhất hoặc có vô số nghiệm.
Ví dụ: Ta có hệ phương trình: \(\begin{cases} x_1 - 2x_2 = -1 \\ -x_1 + 3x_2 = 3 \; \end{cases}\) có nghiệm duy nhất.
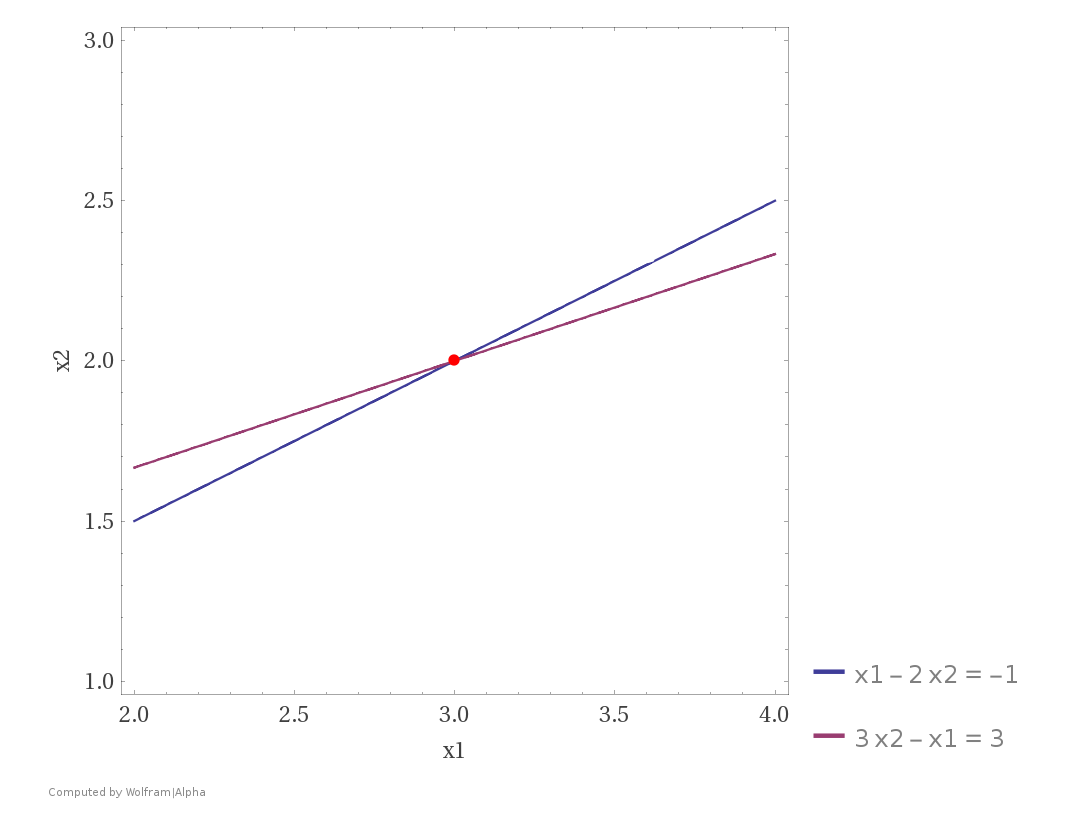
Trong hệ trên hệ pt có cặp nghiệm \((x_1,x_2) = (3,2)\).
Hệ phương trình: \(\begin{cases} x_1 - 2x_2 = -1 \\ -x_1 + 2x_2 = 3 \; \end{cases}\) không có nghiệm.
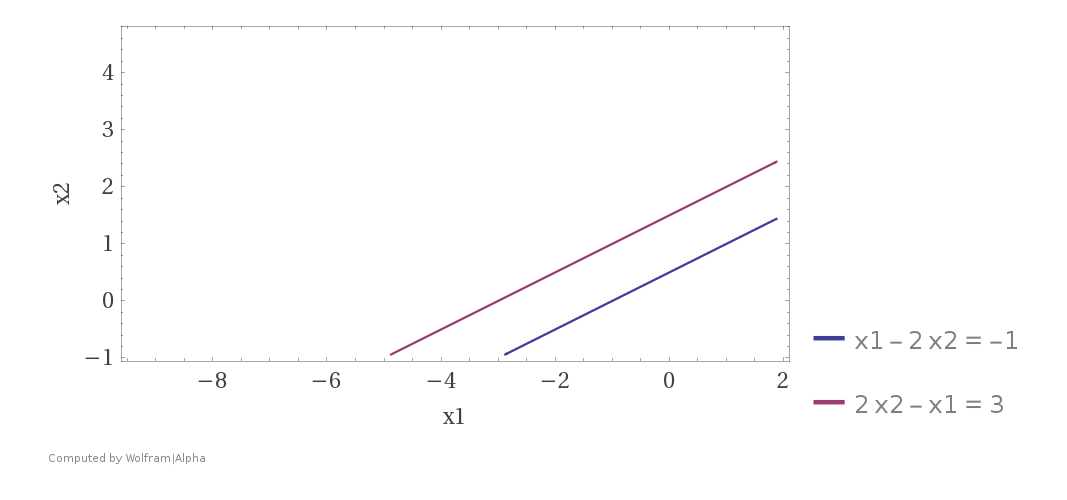
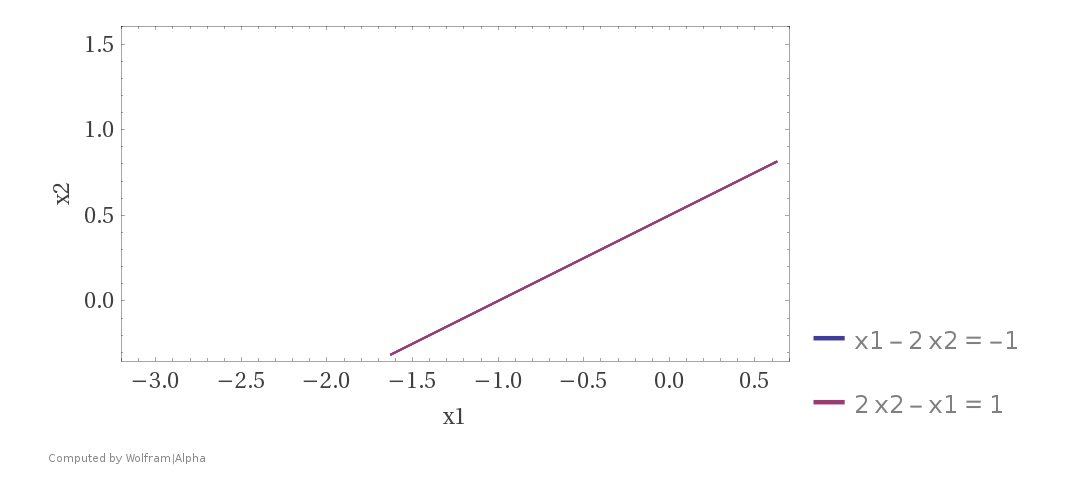
Hệ phương trình: \(\begin{cases} x_1 - 2x_2 = -1 \\ -x_1 + 2x_2 = 1 \; \end{cases}\) có vô số nghiệm.
Một hệ phương trình được gọi là thoả mãn nếu chúng hoặc có một nghiệm hoặc vô số nghiệm, hệ pt không thoả mãn nếu chúng vô nghiệm.
Kí hiệu ma trận
Các thông tin cần thiết của một hệ phương trình tuyến tính có thể ghi lại gọn trong một hình chữ nhật bao gồm các hệ số của hệ phương trình được gọi là ma trận. Ta có hệ pt sau:
\[
\left\{
\begin{array}{ll}
x_1 - 2x_2 + x_3 &= 0 \
2x_2 - 8x_3 &= 8 \
5x_1 -5x_3 &= 10
\end{array}
\right.
\tag{3}\]
Với các hệ số tương ứng với các biến của các cột như sau: \(\begin{bmatrix}1 & -2 & 1 \\ 0 & 2 & -8 \\ 5 & 0 & -5 \end{bmatrix}\) ma trận các hệ số của hệ pt (3).
Và ma trận \(\begin{bmatrix}1 & -2 & 1 & 0 \\ 0 & 2 & -8 & 8 \\ 5 & 0 & -5 & 10 \end{bmatrix}\) (4) được gọi là ma trận bổ sung của hệ.
Chú ý: Ở hàng 2 và hàng 3 của các ma trận trên có các phần tử 0 tương ứng với các hệ số tương ứng với các biến \(x_1\) và \(x_2\) của phương trình (2) và (3) của hệ (3) nhưng không được xuất hiện. Cụ thể ta có thể viết lại pt (2) và (3) của hệ (3) như sau: \(0x_1+2x_2-8x_3 = 8\) và \(5x_1+0x_2-5x_3 = 10\). Ma trận bổ sung bên trên có thêm cột bên phải là các hằng số bên phải của các phương trình trong hệ.
Kích thước của ma trận được thể hiện thông qua các chỉ số hàng và cột mà ma trận có. Ma trận (4) có 3 hàng và 4 cột được gọi là ma trận 3 nhân 4 (3 by 4).
Giải hệ phương trình tuyến tính
Giải hệ phương trình tuyến tính (3)
Lời giải: Thực hiện thủ tục khử (loại bỏ) được biểu hiện bằng hệ phương trình và ma trận hệ số của hệ phương trình song song để dễ dàng so sánh.
\[
\left\{
\begin{array}{ll}
x_1 - 2x_2 + x_3 &= 0 \
2x_2 - 8x_3 &= 8 \
5x_1 - 5x_3 &= 10
\end{array}
\right. \; \; \; \; \;
\begin{bmatrix}1 & -2 & 1 & 0 \\ 0 & 2 & -8 & 8 \\ 5 & 0 & -5 & 10 \end{bmatrix}\]
Giữ nguyên \(x_1\) của phương trình đầu tiên cà thực hiện phương pháp khử (loại bỏ) nó từ các phương trình khác trong hệ. Để làm được điều đó ta tiến hành cộng \((-5)\) với phương trình (1) với phương trình (3).
\[\begin{align}-5.[pt1] \\ + [pt2] \\ [pt3 \; mới]\end{align}\; \; \; \; \;
\left\{
\begin{array}{ll}
5x_1 + 10x_2 - 5x_3 &= 0 \
5x_1 - 5x_3 &= 10 \
10x_2 - 10x_3 &= 10
\end{array}
\right.\]
Kết quả của việc tính toán trên được viết thay thế pt3 của hệ.
\[
\left\{
\begin{array}{ll}
x_1 - 2x_2 + x_3 &= 0 \
2x_2 - 8x_3 &= 8 \
10x_2 - 10x_3 &= 10
\end{array}
\right. \; \; \; \; \;
\begin{bmatrix}1 & -2 & 1 & 0 \\ 0 & 2 & -8 & 8 \\ 0 & 10 & -10 & 10 \end{bmatrix}\]
Bây giờ nhân phương trình (2) của hệ với \(1\over2\) theo thứ tự ta thu được hệ số của \(x_2\) là 1.
\[
\left\{
\begin{array}{ll}
x_1 - 2x_2 + x_3 &= 0 \
x_2 - 4x_3 &= 4 \
10x_2 - 10x_3 &= 10
\end{array}
\right. \; \; \; \; \;
\begin{bmatrix}1 & -2 & 1 & 0 \\ 0 & 1 & -4 & 4 \\ 0 & 10 & -10 & 10 \end{bmatrix}\]
Sử dụng \(x_2\) của phương trình (2) để khử \(10x_2\) của phương trình (3).
\[\begin{align}-10.[pt2] \\ + [pt3] \\ [pt3 \; mới]\end{align}\; \; \; \; \;
\begin{cases}
-10x_2 + 40x_3 &= -40 \
10x_2 - 10x_3 &= 10 \
30x_3 &= -30
\end{cases}
\]
Kết quả của việc tính toán trên ta thu được phương trình thứ 3 mới của hệ.
\[
\left\{
\begin{array}{ll}
x_1 - 2x_2 + x_3 &= 0 \
x_2 - 4x_3 &= 4 \
30x_3 &= -30
\end{array}
\right. \; \; \; \; \;
\begin{bmatrix}1 & -2 & 1 & 0 \\ 0 & 1 & -4 & 4 \\ 0 & 0 & 30 & -30 \end{bmatrix}\]
Bây giờ tiếp tục nhân phương trình (3) với \(1\over30\) ta thu được hệ số 1 của \(x_3\).
\[
\left\{
\begin{array}{ll}
x_1 - 2x_2 + x_3 &= 0 \
x_2 - 4x_3 &= 4 \
x_3 &= -1
\end{array}
\right. \; \; \; \; \;
\begin{bmatrix}1 & -2 & 1 & 0 \\ 0 & 1 & -4 & 4 \\ 0 & 0 & 1 & -1 \end{bmatrix}\]
Hệ phương trình tuyến tính mới ta thu được có dạng tam giác.
Cuối cùng, loại bỏ \(-2x_2\) của phương trình (1), nhưng để hiệu quả hơn ta sử dụng \(x_3\) của phương trình (3) trước, ta tiến hành loại bỏ \(-4x_3\) và \(+x_3\) của phương trình (2) và (1). Dưới đây là miêu tả việc tính toán đó:
\(
\begin{align}4.[pt3] \\ + [pt2] \\ [pt2 \; mới]\end{align}
\begin{cases}
4x_3 &= -4 \
x_2 - 4x_3 &= 4 \
x_2 &= 0
\end{cases}
\)
\(\;\;\;\)
\(
\begin{align}-1.[pt3] \\ + [pt1] \\ [pt1 \; mới]\end{align}
\begin{cases}
-x_3 &= 1 \
x_1 - 2x_2 + x_3 &= 0 \
x_1 - 2x_2 &= 1
\end{cases}
\)
Kết quả ta thu được:
\[
\left\{
\begin{array}{ll}
x_1 - 2x_2 &= 1 \
x_2 &= 0 \
x_3 &= -1
\end{array}
\right. \; \; \; \; \;
\begin{bmatrix}1 & -2 & 0 & 1 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & -1 \end{bmatrix}\]
Ta đã tìm được \(x_3\) ở phương trình (3) và sử dụng \(x_2\) của phương trình (2) để khử \(-2x_2\) của phương trình (1) bằng cách cộng 2 lần phương trình (2) với phương trình (1) ta thu được:
\[
\left\{
\begin{array}{ll}
x_1 &= 1 \
x_2 &= 0 \
x_3 &= -1
\end{array}
\right. \; \; \; \; \;
\begin{bmatrix}1 & 0 & 0 & 1 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & -1 \end{bmatrix}\]
Như vậy hệ phương trình đã cho có nghiệm duy nhất và có rất nhiều cách khác nhau để tính toán, loại bỏ các hệ số trong hệ có thể dùng để tìm nghiệm của hệ. Để kiểm tra lại xem nghiệm tìm được có chính xác không ta thế các giá trị \((x_1,x_2,x_3)\) vừa tìm được vào bên trái của hệ xem kết quả có đúng bằng phía bên phải là các giá trị trong cột bổ sung của ma trận hay không.
\[\begin{align}1 - 2(0) + 1(-1) &= 0\\ 2(0) -8(-1) &= 8\\ 5(1) - 5(-1) &= 10\end{align}\]
Thao tác khử các hệ số của các phương trình trong hệ (phép khử): Thay thế phương trình(hàng) bằng tổng của chính nó với bội số của hàng khác; hoán đổi hai phương trình (hai hàng); nhân giá trị của phương trình với một hằng số khác không.
Vector Equations
Vector trong \(\mathbb{R}^2\)
Một ma trận chỉ có một cột được gọi là vector cột hay thường gọi là vector. Ví dụ: một vector với hai phần tử
\[\vec u = \begin{bmatrix}3 \\ -1\end{bmatrix}, \vec v = \begin{bmatrix}0.2 \\ 0.3\end{bmatrix}, \vec w = \begin{bmatrix}w_1 \\ w_2\end{bmatrix}\]
Với vector \(w\), \(w_1\) và \(w_2\) là các số thực. Tập hopwj tất cả các vector với hai phần tử được kí hiệu là: \(\mathbb{R}^2\). \(\mathbb{R}\) được kí hiệu như là đại diện cho một phần tử số thực trong vector và số 2 trên thể hiện việc vector có hai phần tử số thực. Hai vector được gọi là bằng nhau nếu phần tử tương ứng của chúng bằng nhau. Vector \(\begin{bmatrix}4 \\ 7\end{bmatrix}\) và \(\begin{bmatrix}7 \\ 4\end{bmatrix}\) là không bằng nhau.
Tổng của hai vector \(\vec u\) và \(\vec v\) thuộc \(\mathbb{R}^2\) thu được bằng cách cộng các phần tử tương ứng của \(\vec u\) và \(\vec v\). Ví dụ:
\[ \begin{bmatrix}1 \\ -2\end{bmatrix} + \begin{bmatrix}2 \\ 5\end{bmatrix} = \begin{bmatrix}1+2 \\ -2+5\end{bmatrix} = \begin{bmatrix}3 \\ 3\end{bmatrix} \]
Nhân số vô hướng \(c\) với một vector bằng cách nhân tương ứng từng phần tử của vector với số vô hướng \(c\) đó. Ví dụ:
\[ \vec u = \begin{bmatrix}3 \\ -5\end{bmatrix} and \; c = 5, cu = 5\begin{bmatrix}3 \\ -5\end{bmatrix} = \begin{bmatrix}15 \\ -25\end{bmatrix} \] số thực \(c\) trong \(cu\) được gọi là scalar giá trị vô hướng.
Biểu diễn trong hình học \(\mathbb{R}^2\)
| Tọa độ điểm | Vectors theo mũi tên |
|---|---|
 |
 |
Quy tắc hình bình hành trong việc công vector.
Nếu vectors \(u\) và \(v\) thuộc \(\mathbb{R}^2\) được thể hiện giống như các điểm trong mặt phẳng thì \(u+v\) tương ứng là đỉnh thứ tư của hình bình hành tạo cùng với ba đỉnh còn lại là \(u\), \(0\) và \(v\). Hình ảnh minh họa dưới đây cho thấy rõ điều đấy:
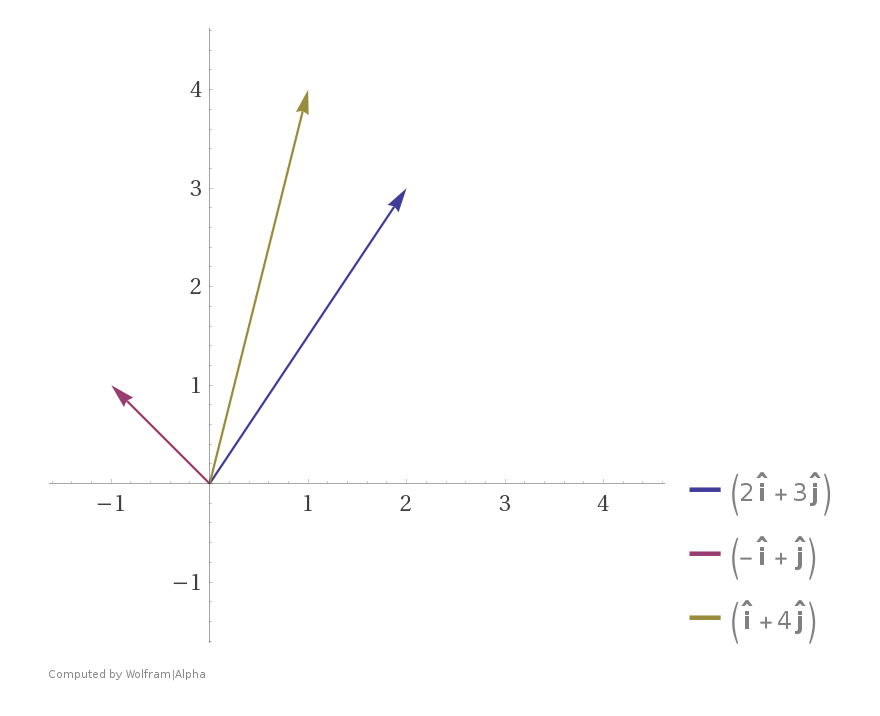
Ở đây các vector \(u = \begin{bmatrix}2 \\ 3\end{bmatrix}\) - vector màu xanh, \(v = \begin{bmatrix}-1 \\ 1\end{bmatrix}\) - vector màu đỏ, \(0 = \begin{bmatrix}0 \\ 0\end{bmatrix}\) - gốc tọa độ và vector \(u+v = \begin{bmatrix}1 \\ 4\end{bmatrix}\) - vector màu vàng.
Vector thuộc \(\mathbb{R}^3\)
Vector thuộc \(\mathbb{R}^3\) là ma trận 3x1 với 3 phần tử. Biểu diễn tương ứng trong hình học là điểm trong hệ tọa độ không gian ba chiều.
Vector thuộc \(\mathbb{R}^n\)
Nếu \(n\) là số nguyên dương, \(\mathbb{R}^n\) là kí hiệu của tập hợp danh sách của \(n\) số thực, thường được viết giống như ma trận cột nx1.
\[ \vec u = \begin{bmatrix}u_1 \\ u_2 \\ . \\ . \\u_n\end{bmatrix} \]
Vector mà tất cả các phần tử của nó bằng 0 được gọi là vector không.
Tổ hợp tuyến tính
Các vetor \(\vec v_1,\vec v_2,…,\vec v_p\) thuộc \(\mathbb{R}^n\) và các số vô hướng \(c_1,c_2,…,c_p\). Vector \(\vec y\) được định nghĩa dưới dạng: \(\vec y = c_1\vec v_1 + c_2\vec v_2 + … + c_p\vec v_p\) được gọi là tổ hợp tuyến tính của \(\vec v_1,\vec v_2,…,\vec v_p\) với các trọng số \(c_1,c_2,…,c_p\). Các trọng số trong tổ hợp tuyến tính có thể là bất kì số thực nào kể cả là 0. Ví dụ: Một vài tổ hợp tuyến tính của hai vector \(\vec v_1, \vec v_2\).
\[ \sqrt{3}\vec v_1 + \vec v_2, \frac{1}{2}\vec v_1 + 0\vec v_2, 0\vec v_1 + 0\vec v_2 \]
\(\mathbf{Ax=b}\)
\[\mathbf{Ax} = \begin{bmatrix}a_1 & a_2 & . & . & a_n\end{bmatrix}\begin{bmatrix}x_1 \\ x_2 \\ . \\ . \\ x_n\end{bmatrix} = a_1x_1 + a_2x_2 + … + a_nx_n\]
\[\mathbf{Ax=b} \sim a_1x_1 + a_2x_2 + … + a_nx_n = b \sim \begin{bmatrix}a_1 & a_2 & . & . & a_n & b\end{bmatrix}\]
Tập nghiệm của hệ phương trình tuyến tính
Hệ thuần nhất có dạng \(\mathbf{Ax=0}\) có nghiệm không tầm thường khi và chỉ khi phương trình có ít nhất một biến tự do(là biến với hệ số bằng không).
Ví dụ: \(\begin{bmatrix}A & 0\end{bmatrix}\)
\[ \begin{bmatrix}3 & 5 & -4 & 0 \\ -3 & -2 & 4 & 0 \\ 6 & 1 & -8 & 0\end{bmatrix} \sim \begin{bmatrix}3 & 5 & -4 & 0 \\ 0 & 3 & 0 & 0 \\ 0 & -9 & 0 & 0\end{bmatrix} \sim \begin{bmatrix}3 & 5 & -4 & 0 \\ 0 & 3 & 0 & 0 \\ 0 & 0 & 0 & 0\end{bmatrix} \]
\[
\begin{bmatrix}1 & 0 & \frac{-4}{3} & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0\end{bmatrix} \; \; \;
\begin{cases}
x_1 - \frac{4}{3}x_3 &= 0 \
x_2 &= 0 \
0 &= 0
\end{cases}
\]
Như vậy ta có \(x_1 = \frac{4}{3}x_3\), \(x_2 = 0\), suy ra \(\mathbf{x} = \begin{bmatrix}x_1 \\ x_2 \\ x_3 \end{bmatrix} = \begin{bmatrix}\frac{4}{3}x_3 \\ 0 \\ x_3 \end{bmatrix} =vx_3\) với \(v=\begin{bmatrix}\frac{4}{3} \\ 0 \\ 1\end{bmatrix}\)
Ta có \(vx_3 = \begin{bmatrix}\frac{4}{3} \\ 0 \\ 1\end{bmatrix}\). Về mặt hình học, tập nghiệm của hệ phương trình là đường thẳng đi qua gốc tọa độ trong \(\mathbb{R}^3\).
Ví dụ: \(10x_1-3x_2-2x_3=0\), suy ra \(x_1=0.3x_2+0.2x_3\).
\[
\mathbf{x} = \begin{bmatrix}x_1 \\ x_2 \\ x_3 \end{bmatrix} = \begin{bmatrix}0.3x_2+0.2x_3 \\ x_2 \\ x_3 \end{bmatrix} = \begin{bmatrix}0.3x_2 \\ x_2 \\ 0 \end{bmatrix} + \begin{bmatrix}0.2x_3 \\ 0 \\ x_3 \end{bmatrix}
\]
\[ \mathbf{x} = x_2\begin{bmatrix}0.3 \\ 1 \\ 0 \end{bmatrix} + x_3\begin{bmatrix}0.2 \\ 0 \\ 1 \end{bmatrix} \]
Như vậy tập nghiệm của pt là tổ hợp tuyến tính của hai vector \(u\) và \(v\) với \(u=\begin{bmatrix}0.3 \\ 1 \\ 0 \end{bmatrix}\) và \(v=\begin{bmatrix}0.2 \\ 0 \\ 1 \end{bmatrix}\) hay \(span{u,v}\) hay mặt phẳng đi qua gốc tọa độ chứa \(u\) và \(v\).
Tập nghiệm dạng: \(\mathbf{x}=su+tv\) \((s,t\in\mathbb{R})\).
Nghiệm của hệ không thuần nhất
\(w=p+v_h\) trong đó \(v_h\) là nghiệm của \(\mathbf{Ax=0}\).
Độc lập tuyến tính
Tập \(\{v_1,v_2,\ldots,v_p\}\in\mathbb{R}\) được gọi là độc lập tuyến tính nếu pt:
\[ x_1v_1+x_2v_2+\cdots+x_pv_p=0 \]
chỉ có nghiệm tầm thường và phụ thuộc tuyến tính nếu tồn tại các trọng số \(c_1,c_2,\ldots,c_p\) không đồng thời bằng \(0\)
\[ c_1v_1+c_2v_2+\cdots+c_pv_p=0 \]